Python

Python-迴歸分析

相關係數,線性迴歸, statsmodels, sklearn, itertools

相關係數

rets.corr()

Ctrip Lion
Ctrip 1.000000 0.059657
Lion 0.059657 1.000000

簡單線性迴歸(LinearRegression)

1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.linear_model import LinearRegression
X1 = X.iloc[0:len(X)].to_frame() #Convert Series to DataFrame
Y1 = Y.iloc[0:len(Y)].to_frame()
regr = LinearRegression()
regr.fit(X1,Y1)
regr.coef_ #係數
regr.intercept_ #截距
regr.predict(X1) #依線性迴歸公式計算Y值
% pylab inline #繪製散佈圖
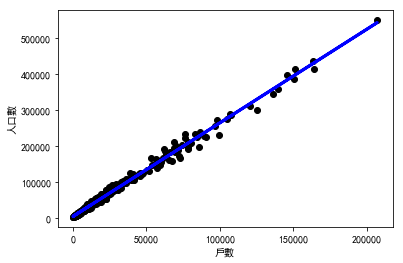
plt.scatter(X1,Y1, color="black")
plt.xlabel('戶數',fontproperties='SimHei')
plt.ylabel('人口數',fontproperties='SimHei')

$$ Y = \beta_0+\beta_1X $$
戶數與人口散佈圖

錯誤訊息：
執行regr.fit時，產生異常訊息
Found input variables with inconsistent numbers of samples: [1, 368]
處理方式：
錯誤原因是sklearn要求使用DataFrame，但原資料為Series，所以將資料重新reshape即可使用X.iloc[0:len(X)].to_frame()

  • series 是一維的數據類型，dataframe 是一個二維的、表格型的數據結構。

多變量線性迴歸

`線性迴歸也被稱為最小二乘法回歸（Linear Regression, also called Ordinary Least-Squares (OLS) Regression）

sklearn

1
2
3
4
5
6
7
8
9
10
house = pd.read_csv('python_for_data_science-master/Data/house-prices.csv')
house1 = pd.concat([house,pd.get_dummies(house['Brick']),pd.get_dummies(house['Neighborhood'])],axis=1)
del house1['Home'], house1['No'], house1['Brick'], house1['Neighborhood']
X = house1[['SqFt', 'Bedrooms', 'Bathrooms', 'Offers', 'Yes', 'East', 'North', 'West']]
Y = house1['Price'].values
from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X,Y)
house1['Price_Predict'] = regr.predict(X).astype(int)
house1.head()
Price SqFt Bedrooms Bathrooms Offers Yes East North West Price_Predict
0 114300 1790 2 2 2 0 1 0 0 103182
1 114200 2030 4 2 3 0 1 0 0 116127
2 114800 1740 3 2 1 0 1 0 0 113047
3 94700 1980 3 2 3 0 1 0 0 109230
4 119800 2130 3 3 3 0 1 0 0 125063

statsmodels

參數估計：
矩估計（Method of Moment、MOM）
最小平方法（Ordinary Least Square Estimation, OLSE）
最大似然估計（Maximum Likelihood Estimation, MLE）

1
2
3
4
5
import statsmodels.api as sm
X2 = sm.add_constant(X) #為模型增加常數項，即迴歸線在y軸上的截距
est = sm.OLS(Y, X2)
est2 = est.fit()
print (est2.summary())

  • sklearn,statsmodels計算之結果是相同的

regr.coef_
array([ 52.99374081, 4246.79389165, 7883.27849293, -8267.48831831,
17297.34952752, -22241.61647014, -20681.03735068])

regr.intercept_
22840.535538009528

est2.params
const 22840.535538
SqFt 52.993741
Bedrooms 4246.793892
Bathrooms 7883.278493
Offers -8267.488318
Yes 17297.349528
East -22241.616470
North -20681.037351
dtype: float64

  • 赤池信息準則 AIC (Akaike Information Criterion) 評估統計模型的複雜度和衡量統計模型「擬合」資料之優良性的一種標準，尋找可以最好地解釋數據但包含最少自由參數的模型，優先考慮的模型應是AIC值最小的那一個
    $$ AIC = 2K - 2\ln(L) $$
    K是參數的數量，L是似然函數
    當模型複雜度提高（k增大）時，似然函數L也會增大，從而使AIC變小，但是k過大時，似然函數增速減緩，導致AIC增大，模型過於複雜容易造成過擬合現象。

  • 貝葉斯信息準則 SIC (Schwartz Information Criterion)

itertools應用

1
2
3
4
5
6
7
8
9
10
11
12
13
predictorcols = ['SqFt', 'Bedrooms', 'Bathrooms', 'Offers', 'Yes', 'East', 'North']
import itertools
AICs = {}
for k in range(1,len(predictorcols)+1):
    for variables in itertools.combinations(predictorcols, k): 
        predictors  = X[list(variables)]
        predictors2 = sm.add_constant(predictors)
        est = sm.OLS(Y, predictors2)
        res = est.fit()
        AICs[variables] = res.aic
from collections import Counter
c = Counter(AICs)
c.most_common()[::-10] #x[startAt:endBefore:skip]
  • itertools迭代指重覆取值，重覆反饋過程的活動
    itertools.combinations(['A','B','C','D'],2)可以得到AB,AC,AD,BC,BD,CD

羅吉斯迴歸 (Logistic Regression)

1
2
3
4
5
6
7
8
============== ==== ==== ======= ===== ====================
                Min  Max   Mean    SD   Class Correlation
============== ==== ==== ======= ===== ====================
sepal length:   4.3  7.9   5.84   0.83    0.7826
sepal width:    2.0  4.4   3.05   0.43   -0.4194
petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
petal width:    0.1  2.5   1.20  0.76     0.9565  (high!)
============== ==== ==== ======= ===== ====================

上述為iris資料庫之描述性統計資料，下面取petal length及petal width使用，分別取最小值及最大值後加減1，並進行meshgrid處理
(0, 7.9, 0.1)
(-0.9, 3.5, 0.1) –> 44個區間(-0.9, -0.8, -0.7,…..3.4)
XX即為[ 0. , 0.1, 0.2, …. 7.6, 7.7, 7.8]共44個
yy即為[-0.9, -0.9, -0.9, …. -0.9, -0.9, -0.9][-0.8, -0.8, -0.8, …. -0.8, -0.8, -0.8]…..[3.4, 3.4, 3.4, …. 3.4, 3.4, 3.4]
Z即為依據xx,yy資料產出之決策樹預測結果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn import tree
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
#圖形中文顯示處理
matplotlib.rc('font', **{'sans-serif' : 'SimHei',
                       'family' : 'sans-serif'})
def plot_estimator(estimator, X, y, title):
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 ##加1減1只是為了繪圖時留空白
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                         np.arange(y_min, y_max, 0.1)) #meshgrid根據坐標向量創建坐標矩陣
    Z = estimator.predict(np.c_[xx.ravel(), yy.ravel()]) #一維,共3476筆資料
    #ravel() Return a contiguous flattened array
	#np.c_ 串接兩個list,np.ravel將矩陣變為一維
	Z = Z.reshape(xx.shape) #二維,共44筆資料(44,79)
    plt.plot()
	#Contours(輪廓) can be explained simply as a curve joining all the continuous points (along the boundary), having same color or intensity.
    plt.contourf(xx, yy, Z, alpha=0.4, cmap = plt.cm.RdYlBu) #cmap- Colormap #alpha透明度,愈小愈透明0~1
    plt.scatter(X[:, 0], X[:, 1], c=y,  cmap = plt.cm.brg) #c - color
    plt.title(title)
    plt.xlabel('Petal.Length')
    plt.ylabel('Petal.Width')
    plt.show()
iris = load_iris()
X = iris.data[:,[2,3]]
y = iris.target[:]
#決策樹DecisionTree
clf = tree.DecisionTreeClassifier()
clf.fit(X, y)
#支援向量機SVM
clf1 = SVC(kernel="linear")
clf1.fit(X, y)
#羅吉斯迴歸
clf2 = LogisticRegression()
clf2.fit(X, y)
#隨機森林
clf3 = RandomForestClassifier(n_estimators=100, criterion="entropy", random_state=0)
clf3.fit(X, y)
plot_estimator(clf, X, y, "決策樹")
plot_estimator(clf1, X, y, "支援向量機")
plot_estimator(clf2, X, y, "羅吉斯迴歸")
plot_estimator(clf3, X, y, "隨機森林")

決策樹模型
支援向量機模型
羅吉斯迴歸模型
隨機森林模型

The C parameter tells the SVM optimization how much you want to avoid misclassifying each training example. For large values of C, the optimization will choose a smaller-margin hyperplane if that hyperplane does a better job of getting all the training points classified correctly. Conversely, a very small value of C will cause the optimizer to look for a larger-margin separating hyperplane, even if that hyperplane misclassifies more points. For very tiny values of C, you should get misclassified examples, often even if your training data is linearly separable.

傳統線性迴歸的迴歸係數（regression coefficient）的解釋為「當自變項增加一個單位，依變項則會增加多少單位」，但是在Logistic regression的迴歸係數解釋為「當自變項增加一個單位，依變項1相對依變項0的機率會增加幾倍」，也就是說「自變項增加一個單位，依變項有發生狀況（習慣稱為Event）相對於沒有發生狀況（non-event）的比值」，這個比值就是勝算比（Odds ratio, OR）。我們可以這樣說，除了迴歸係數的解釋方法不太相同之外，基本上可說傳統線性迴歸跟Logistic regression是一樣的分析。
from 晨晰統計

顧客忠誠度分析

1
2
3
4
5
6
	state	account_length	area_code	international_plan	voice_mail_plan	number_vmail_messages	total_day_minutes	total_day_calls	total_day_charge	total_eve_minutes	total_eve_calls	total_eve_charge	total_night_minutes	total_night_calls	total_night_charge	total_intl_minutes	total_intl_calls	total_intl_charge	number_customer_service_calls	churn
1	KS	128	area_code_415	no	yes	25	265.1	110	45.07	197.4	99	16.78	244.7	91	11.01	10.0	3	2.70	1	no
2	OH	107	area_code_415	no	yes	26	161.6	123	27.47	195.5	103	16.62	254.4	103	11.45	13.7	3	3.70	1	no
3	NJ	137	area_code_415	no	no	0	243.4	114	41.38	121.2	110	10.30	162.6	104	7.32	12.2	5	3.29	0	no
4	OH	84	area_code_408	yes	no	0	299.4	71	50.90	61.9	88	5.26	196.9	89	8.86	6.6	7	1.78	2	no
5	OK	75	area_code_415	yes	no	0	166.7	113	28.34	148.3	122	12.61	186.9	121	8.41	10.1	3	2.73	3	no

電信公司之客戶忠誠度分析資料

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import pandas
import numpy
from sklearn import tree
from sklearn.tree import export_graphviz
import graphviz
import pydotplus
#讀入資料
df = pandas.read_csv('python_for_data_science-master/Data/customer_churn.csv', index_col=0, header = 0)
df = df.iloc[:,3:]
#將yes/no資料轉換為1/0
cat_var = ['international_plan','voice_mail_plan', 'churn']
for cat in cat_var:
    df[cat] = df[cat].map(lambda e: 1 if e == 'yes' else 0)
#將churn欄位歸為y,其餘欄位為X
y = df.iloc[:,-1]
X = df.iloc[:,:-1]
#使用決策樹分析
dt = tree.DecisionTreeClassifier(max_depth=3)
dt.fit(X, y)
#計算準確率
print (numpy.sum(y== dt.predict(X)) / len(y))
# 繪製決策樹圖
dot_data = tree.export_graphviz(dt, out_file=None, 
                     filled=True, rounded=True,  
                     special_characters=True)  
graph = pydotplus.graph_from_dot_data(dot_data)  
Image(graph.create_png())

顧客忠誠度分析

正確率的計算方法有二
1.使用from sklearn.metrics import accuracy_score套件 accuracy_score(iris.target, predicted)
2.直接sum()計算　numpy.sum(y== dt.predict(X)) / len(y)

混洧矩陣
from sklearn.metrics import confusion_matrix
confusion_matrix(iris.target, predicted)

不同的正確率計算方式
from sklearn.metrics import classification_report
print(classification_report(iris.target, predicted))

precision recall f1-score support
0 1.00 1.00 1.00 50
1 0.98 0.90 0.94 50
2 0.91 0.98 0.94 50
avg / total 0.96 0.96 0.96 150